Klaus Rohwer 

Welche Schwingungsformen kann eine Stimmzunge (theoretisch) annehmen?

beruflich...
Links 
Kontakt 

Mein kleiner Beitrag zur Physik der durchschlagenden Stimmzunge: ich habe ein numerisches Modell einer Stimmzunge erstellt und ihre Schwingungsformen -- fachlich Moden genannt -- mit der Finite-Elemente-Methode (FEM) berechnet. Das Modell entstand als selbstgestellte Übungsaufgabe im Rahmen der Teilnahme an einem Lehrgang zur Einführung in das FEM-Pre- und -Postprozessor-Programm MEDINA bei T-Systems in Leinfelden bei Stuttgart.

1. Schwingungsmode = 1. vertikale Transversalmode = Grundschwingung	2. Schwingungsmode = 2. vertikale Transversalmode	3. Schwingungsmode = 1. horizontale Transversalmode	4. Schwingungsmode = 3. vertikaleTransversalmode	5. Schwingungsmode = 1. Torsionsmode
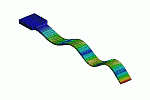6. Schwingungsmode = 4. vertikaleTransversalmode	7. Schwingungsmode = 2. horizontale Transversalmode	8. Schwingungsmode = 2. Torsionsmode	9. Schwingungsmode = 5. vertikaleTransversalmode	15. Schwingungsmode = 1. Longitudinalmode

Für bewegte und vergrößerte Bilder und für Erklärungen zu den einzelnen Moden bitte auf das betreffende Bild klicken!

Ein physikalisches System wie eine Stimmzunge kann prinzipiell drei Arten von Schwingungen ausführen:

• Longitudinale (Längs-),
• transversale (Quer-) und
• Torsions(Dreh-)schwingungen.

Von den transversalen Schwingungen gibt es zwei Arten: horizontale (waagerechte) und vertikale (senkrechte). Die normale Art zu schwingen ist transversal-vertikal, und die erste Transversalmode ist auch die Grundschwingung der Stimmzunge. An einer realen Mundharmonika ist es mir mit einer speziellen Apparatur gelungen, (nicht nur) die Grundschwingung von Stimmzungen zu filmen.

Torsionsschwingungen und horizontale Transversalmoden sollen eigentlich nicht auftreten, tun es aber manchmal dennoch und machen sich als "Quietschen" oder "Klingeln" bemerkbar. Auch die Torsionsschwingung habe ich an einer realen Stimmzunge filmen können.

Theoretisch gibt es unendlich viele Schwingungsmoden. Ich habe die ersten (niedrigsten) fünfzehn Schwingungsmoden berechnet, und es sind alle genannten Schwingungsformen darunter. Ich gebe hier nur die ersten neun sowie die fünfzehnte wieder, denn die Moden zehn bis vierzehn sind bereits so hochfrequent, dass sie jenseits der Hörgrenze des Menschen liegen. Außerdem sind sie relativ uninteressant: es handelt sich um Wiederholungen niedrigerer Moden mit erhöhter "Knotenzahl" (was das ist, sieht man bei den einzelnen Moden).

Mir standen bei der Modellerstellung keine exakten Daten realer Stimmzungen zur Verfügung, daher habe ich für die Abmessungen, die die Schwingungsfrequenzen entscheidend beeinflussen, Schätzwerte verwendet bzw. früher einmal gemessene Werte aus dem Gedächtnis rekonstruiert. (Ich hatte zwar eine Mundharmonika dabei, aber leider keine Schiebelehre, geschweige denn eine Mikrometerschraube...) Mir ist es zwar gelungen, die Grundschwingung auf 443 Hz (a') zu bringen, aber dafür, wie die höheren Schwingungsfrequenzen im Verhältnis zur Grundschwingung stehen, übernehme ich keine Gewähr!

In der Praxis werden auch heute noch die Frequenzen der Stimmzungen durch die Erfahrungen derjenigen Menschen bestimmt, die die Stimmzungen fräsen, und nicht durch numerische Berechnungen. Die numerische Berechnung der Frequenzen scheitert daran, dass man die Materialeigenschaften nicht genau genug kennt. Diese verändern sich ja auch während der Bearbeitung noch! Durch das Fräsen und Stanzen der Stimmzungen wird die Mikrostruktur des Stimmzungenmaterials verändert, und dadurch verändert sich auch die Elastizität, die ja die Schwingungsfrequenz mitbestimmt. Sie ist zum Beispiel auf der Unterseite der Stimmzunge anders als auf der Oberseite, aber kaum messbar. Das macht die Berechnung mit der geforderten Genauigkeit praktisch unmöglich.

Die Inhalte meiner Kleinen Mundharmonikaphysik finden sich auch - ausführlicher und aktualisiert - in meinem 2022 erschienenen Mundharmonikabuch. Für die Schwingungsmoden der Stimmzungen verweise ich dort allerdings auf diese Seite.