Klaus Rohwer
Startseite
privat...
Hobbies:
Schaltungssammlung
|
Kapazitätsmessung
Der untenstehende Text war die Grundlage für einen Artikel in der Zeitschrift Elektor ("Einfaches Kapazitätsmeßgerät", Elektor 300, S. 65, 1995; ebenfalls erschienen in Elektor Electronics (GB)).
Genaue Kapazitätsmessung - ganz einfach
Viele Schaltungen zur Kapazitätsmessung benötigen zum Abgleich einen Referenzkondensator mit möglichst genau bekannter Kapazität. Solche sind aber schwer erhältlich und nicht gerade preiswert. Wer über einen Frequenzzähler mit Pulsdauermeßfunktion verfügt, kann mit ein wenig Überlegung sehr genaue Kapazitätsmessungen auch ohne einen Referenzkondensator ausführen.
Lädt man einen unbekannten Kondensator Cx mit einem bekannten Konstantstrom I0 auf, so ändert sich die Spannung über Cx linear mit der Zeit t gemäß:
Ux = I0 /Cx · t,
d. h. um eine bestimmte Spannung zu erreichen, braucht man eine Zeit, die
der
Kapazität proportional ist. Sind Strom und Spannung bekannt, so kann aus
der gemessenen Zeit die Kapazität berechnet werden.
Eine entsprechende Schaltung könnte aussehen wie in Bild 1: Eine Konstantstromquelle, die genau 1µA liefert, lädt Cx auf. Währenddessen liefert die Schaltung um A1 und A2 einen Impuls, der
bei Überschreiten einer unteren Spannungsschwelle beginnt und bei
Überschreiten einer oberen, genau 1V höher liegenden Schwelle endet.
Die Impulsdauer kann mit einem entsprechend eingestellten Frequenzzähler
sehr genau gemessen werden und beträgt nach der obigen Formel eine
Millisekunde pro Nanofarad.
Die Präzision der Kapazitätsmessung kann so zurückgeführt
werden auf die Genauigkeiten der Strom-, Spannungs- und Zeitmessung. Diese sind
im Digitalzeitalter sehr hoch.
Es geht jedoch noch viel einfacher! Die Schaltung in Bild 1 erinnert an das
Innenleben eines 555-Timer-ICs, und tatsächlich läßt sich damit
leicht eine derartige Schaltung aufbauen. Man kommt sogar ohne eine
Konstantstromquelle aus, wenn man sich die Mühe macht, ein wenig zu
rechnen: Die Aufladung von Cx erfolgt gemäß einer Exponentialfunktion (Bild 2)
Ux (t) = UB (1 - exp(-t/RCx)), (1)
wenn R der Ladewiderstand zwischen Cx und +UB ist.
Die Schaltschwellen von IC1 liegen bei 1/3 UB und bei 2/3 UB, daher gilt zu den Zeitpunkten t1 und t2:
Ux (t1) = 1/3 UB, (2)
Ux (t2) = 2/3 UB. (3)
Einsetzen in (1) liefert:
| exp (-t1/RCx) = 2/3 | ⇒ | t1/RCx = -ln(2/3) | (4) |
| exp (-t2/RCx) = 1/3 | ⇒ | t2/RCx = -ln(1/3) | (5) |
(ln = natürlicher Logarithmus). Setzt man die Impulsdauer Δt = t2 - t1, so ergibt sich
| Δt/RCx = ln(2/3) - ln(1/3) = ln 2. | (6) |
Damit folgt bei gegebenem Verhältnis Δt/Cx :
| R = Δt/(Cx ln2), | (7) |
unabhängig von UB! Für ein Verhältnis von 1 ms/nF ergibt sich R zu 1,4427 MΩ.
Zum Vergrößern bitte auf das Bild klicken! (Öffnet neues
Fenster) - Zu diesem Bild gibt es eine Stückliste.
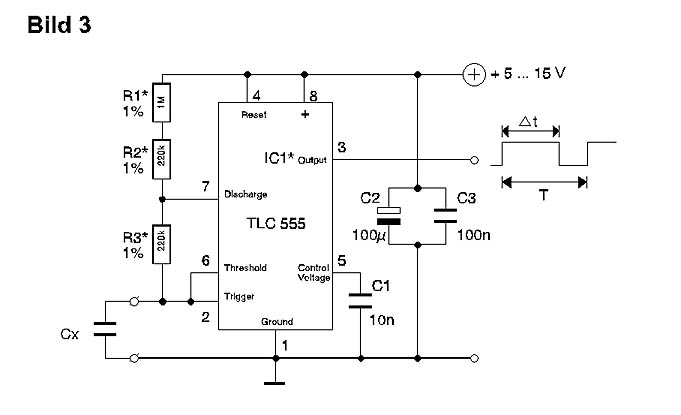
Bild 3 zeigt eine Schaltung, die von diesen Überlegungen Gebrauch macht. Sie
liefert ein periodisches Ausgangssignal, dessen Impulslänge in
Millisekunden die Kapazität von Cx in Nanofarad wiedergibt. R setzt sich aus R1, R2 und R3 zusammen, wobei R3
gleichzeitig die Entladezeit von Cx und damit die Impulspause bestimmt. Damit lassen sich bequem
Kapazitätswerte von ca. 4,7 nF bis zu 1 µF messen, wobei die untere
Grenze vom verwendeten Frequenzzähler bestimmt wird. Nach oben hin gibt es
im Prinzip keine Grenze, wenn man entsprechend lange auf das Ergebnis warten
kann: Die erste Messung nach dem Einschalten bzw. Einstecken von Cx benötigt ca. 2 Δt, bis sich Cx erstmalig auf 2/3 UB aufgeladen hat; der erste angezeigte Wert ist zu verwerfen, weil der
Ausgansimpuls von IC1 nicht erst bei Ux = 1/3 UB, sondern schon bei t = 0 beginnt. Die erste brauchbare Messung dauert dann
nochmals Δt, immerhin 1 Sekunde pro Mikrofarad!
Ein weiterer Nachteil bei der Messung großer Kapazitäten ist die
Verfälschung durch Leckströme bei Elektrolytkondensatoren. Diese
sollten daher mit größeren Ladeströmen beaufschlagt werden, bei
denen ein kleiner Leckstrom nicht so ins Gewicht fällt. Es bietet sich an,
den Strom gleich um einen Faktor tausend zu vergrößern, indem man R1
= 1kΩ und R2 = R3 = 220 Ω setzt, denn dadurch wird Δt/Cx gerade gleich 1 ms/µF.
Damit nicht Eingangsströme von IC1 die Messung beeinflußen,
muß die CMOS-Version des altbekannten 555, der 7555 bzw. TLC555,
gewählt werden. Die absolute Genauigkeit (eigentlich: Ungenauigkeit), die
man so erreichen kann, beträgt aufgrund der Präzision des IC-internen
Spannungsteilers (initial accuracy 1%) und der verwendeten Widerstände R1...R3 ca. 2%, und das ganz ohne
Abgleich! Die relative Genauigkeit (Reproduzierbarkeit) ist wesentlich
höher und wird hauptsächlich durch die Temperaturkoeffizienten der
verwendeten Bauteile bestimmt. Diese Schaltung hat den Vorteil, daß sie
so einfach ist, daß sie sich "mal eben schnell" aus der
Bastelkiste aufbauen läßt.
Zum Vergrößern bitte auf das Bild klicken! (Öffnet neues
Fenster) - Zu diesem Bild gibt es eine Stückliste.
Wer es noch genauer haben möchte...
...kommt ums Abgleichen nicht herum, doch reicht dafür ein
Digitalmultimeter. Das sollte allerdings möglichst mindestens
4½-stellig sein, sonst fällt der Genauigkeitszuwachs recht bescheiden
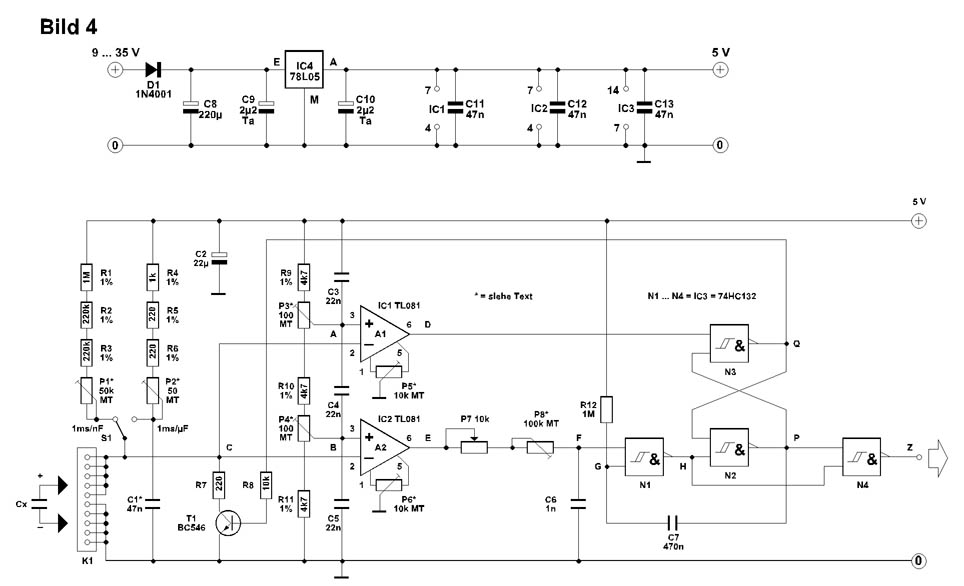
aus (siehe Fehlerrechnung). Die Schaltung in Bild 4 zeigt, daß es sich im wesentlichen um einen diskreten Nachbau des 555
handelt, jedoch nicht ganz: Der Unterschied liegt in den NAND-Gattern N1 und N4
und deren Beschaltung. Bei kleinen Kapazitäten wird bei der Schaltung in Bild 3 nicht nur die Pulslänge Δt kürzer, sondern die Periodendauer T genauso. Daher wird es mitunter
schwierig, die Zahlenwerte auf dem Frequenzzähler abzulesen, weil die
Anzeige nur noch zu flackern scheint. Bei manchen Frequenzzählern kommt
noch hinzu, daß sie bei kurzen Pulspausen Schwierigkeiten mit dem
internen Timing bekommen. Diesem hilft die Kombination R12/C7 ab: sie
verhindert, daß das Flipflop N2/N3 vor Ablauf der Zeitkonstante dieses
RC-Gliedes von A2 neu getriggert werden kann. Die Meßwerte folgen so auch
bei kleinen Cx in gut beobachtbaren Zeitabständen aufeinander. Die Pulsdauer am Ausgang
von N2 verlängert sich dadurch aber um die Zeit, die benötigt wird,
um Cx wieder bis auf die untere Schwellenspannung (1/3 UB) aufzuladen. Damit am Ausgang dennoch das richtige Signal erscheint, stellt N4
eine passende Verknüpfung her. Allerdings dreht sich dadurch die
Polarität des Ausgangssignals um, so daß am Ausgang dieser Schaltung
die Pulspause das Maß für die Kapazität darstellt. Selbstverständlich
kann man auch noch einen Inverter nachschalten, wenn man will.
Auch bei der Messung großer Kapazitäten hat N4 einen vorteilhaften
Einfluß: jetzt stimmt schon der erste angezeigte Meßwert, denn der
Ausgang ist tatsächlich nur so lange low, wie sich Ux zwischen den beiden Spannungsschwellen befindet.
Jetzt zu der Kombination P7/P8/C6: Durch unvermeidbare parasitäre
Kapazitäten gibt es am Ausgang immer Impulse, auch dann, wenn gar kein Cx vorhanden ist. Beim Musteraufbau hatten sie im empfindlicheren
Meßbereich (1ms/nF) eine Dauer von ca. 42 µs, das entspricht 42 pF.
Dies kann man kompensieren, indem man die fallende Flanke am Ausgang von A2 um
diese Zeit verzögert, und genau dazu dient dieses RC-Glied. Daß auch
die steigende Flanke dabei verzögert wird, stört nicht weiter. Im
anderen Meßbereich (1ms/µF) bedeutet die Verzögerung jedoch
eine "parasitäre" Kapazität von 42 nF - und weil die
natürlich normalerweise nicht so groß ist, machen wir sie so
groß: mit C1.
Alles in allem ist die Schaltung nach Bild 4 nicht nur genauer, sondern bietet
auch mehr Komfort.
- Grundlagen - Genauer! - Aufbau - Abgleich
Die Betriebsspannung wurde zu 5 Volt gewählt. Der Grund dafür liegt im Abgleichvorgang (siehe unten): P3 und P4 sind so einzustellen, daß die Betriebsspannung genau gedrittelt wird. Eine Spannung kann dann am genauesten gemessen werden, wenn sie gerade unterhalb einer Bereichsgrenze des verwendeten Meßgeräts liegt. (Dies gilt wegen des Digit-Fehlers auch für Digitalmultimeter.) Der praktikabelste Meßbereich ist in diesem Fall 2 V, so daß die maximale Betriebsspannung knapp 6 V beträgt. Keinesfalls sollte sie aber knapp über 6 V liegen, so daß ein 6-V-Spannungsregler nicht in Frage kommt. Daher wurde für die Spannungsstabilisierung ein 78L05 vorgesehen. Als Energiequelle dient ein(e) 9V-Batterie bzw. -Akku oder ein entsprechendes Steckernetzgerät. Bei Batterieversorgung kann die Verpolungsschutzdiode D1 entfallen, dafür sollte ein Einschalter vorgesehen werden.
Für die meisten Widerstände kommen nur Metallfilmausführungen mit 1% Toleranz (oder besser) in Frage, die Trimmpotis müssen Mehrgang-Cermet-Typen sein. K1, S1 und P7 werden zweckmäßigerweise auf der Frontplatte angebracht. Als Operationsverstärker hat sich der TL081 bewährt, weil er auch bei der niedrigen Versorgungsspannung noch relativ schnell ist (anders als Low-Voltage-Typen wie CA 3140 oder TLC 251).
C1 wird zunächst noch nicht eingelötet, sondern erst nach dem Abgleich (siehe unten).
Als Steckfassung K1 für die Meßobjekte Cx wurde eine 10-polige single-in-line-IC-Fassung verwendet, bei der je 5 Kontakte miteinander verbunden wurden. (Zwei solcher Fassungen verwendet man normalerweise für 20-polige DIL-ICs.) Der Ausgang wird über eine BNC-Buchse nach außen geführt.
Die Punkte A, B, C, D und E sowie Masse und Versorgungsspannung sollten über Lötnägel zugänglich sein. Zusätzlich wird zum Abgleich ein kurzes Kabel mit Steckschuhen für Lötnägel benötigt.
- Grundlagen - Genauer! - Aufbau - Abgleich
Die Schaltung enthält zwar 7 Abgleichpunkte, dennoch ist die Einstellung nicht schwierig. Zunächst werden P7 und P8 auf minimalen Widerstandswert gestellt, alle anderen Trimmpotis bleiben in Mittelstellung. Dann wird der Widerstand der Kombination R1 + R2 + R3 + P1 auf genau den errechneten Wert von 1,4427 MΩ eingestellt, R4 + R5 + R6 + P2 entsprechend auf 1,4427 kΩ. Das geht am besten, wenn sich S1 in der jeweils gerade anderen Position befindet.
Anschließend wird die Versorgungsspannung angelegt. Sodann mißt man im 2-V-Bereich eines Digitalvoltmeters die drei Spannungen am Spannungsteiler R4/P2/R5/P3/R6 (Masse - Punkt B, Punkt A - Punkt B und Punkt A - +UB) und addiert sie. Dies ergibt einen genaueren Wert für die tatsächlich anliegende Versorgungsspannung, als wenn man sie (im 20-V-Bereich) direkt mißt. Diesen Wert teilt man dann wieder durch drei, um den Sollwert für die Spannungen an den Opamp-Eingängen zu erhalten. Diese Spannung, gemessen gegenüber +UB, stellt man dann mit P3 an Punkt A ein, anschließend nochmals denselben Wert mit P4 an Punkt B, diesmal gemessen gegenüber Punkt A.
Es folgt der Offset-Abgleich der Operationsverstärker: Dazu wird zunächst der invertierende Eingang von A1 mit dem nichtinvertierenden verbunden (Punkt A mit C). An Punkt D (Ausgang von A1) und Masse wird ein Voltmeter angeschlossen. Durch Drehen an P5 stellt man dann die Ausgangsspannung auf die Hälfte der Versorgungsspannung ein. Das gleiche wird mit A2 und P6 wiederholt, nachdem man die Verbindung zwischen den Opamp-Eingängen entsprechend umgesteckt hat (Punkt B mit C verbunden).
Jetzt kann man einen Frequenzzähler an den Ausgang anschließen, den man in den Modus "Zeitmessung" versetzt. Bei dieser Schaltung ist - wie oben schon gesagt - darauf zu achten, daß der Zähler so eingestellt ist, daß er die Dauer der Pulspause anzeigt. Ohne daß ein Meßobjekt Cx angeschlossen ist, wird im 1 ms/nF-Meßbereich (Stellung von S1 wie im Schaltplan) jetzt eine Pulspausendauer von einigen zehn Mikrosekunden auf der Anzeige erscheinen. Dies ist einerseits die zu kompensierende parasitäre Kapazität (in Pikofarad), andererseits aber auch der Wert (in Nanofarad) des Kondensators C1, der im anderen Meßbereich eine entsprechende parasitäre Kapazität simuliert. Diese Zahl wird für später notiert.
Jetzt kommt P7 in Mittelstellung, und mit P8 wird die Zahl auf der Anzeige des Frequenzzählers so weit verkleinert, daß sie gerade Null erreicht.
Damit ist der Abgleich eigentlich schon beendet und die genaue Messung von Kapazitäten kann beginnen, und zwar im Bereich von einigen Pikofarad bis zu mehreren Mikrofarad. Aber das Meßgerät ist noch nicht fertig, denn es fehlt noch C1! Die erste Messung, die wir ausführen, ist die Messung der Kapazität eines Kondensators, der als C1 vorgesehen ist. Sein Wert in Nanofarad sollte möglichst genau so groß sein, wie der oben notierte Zahlenwert. Dazu nimmt man am besten eine Anzahl von Kondensatoren des nächstliegenden Normwertes (bei 42 µs z.B. 47 nF) her und wählt anhand der Meßwerte den passendsten aus. Genaue Übereinstimmung ist gar nicht nötig, denn mit P7 kann man in beiden Meßbereichen einen exakten Nullabgleich über einen Bereich von ca. ±10 µs durchführen.
Wenn das so ausgewählte C1 eingelötet ist, ist das Meßgerät endgültig fertig und erlaubt Messungen bis weit in den Millifaradbereich hinein.
Zum Nullabgleich ist nach dem Einschalten und nach jedem Bereichswechsel zunächst P7 auf minimalen Widerstandswert einzustellen und dann so lange zu verdrehen, bis die Anzeige gerade so eben Null erreicht. Dreht man zu weit, so werden kleine Kapazitäten im Pikofarad- bzw. Nanofaradbereich überhaupt nicht mehr erkannt, und das Meßergebnis wird um denselben Betrag verfälscht.
Es sollte darauf geachtet werden, daß die Meßobjekte vor dem Anschluß an das Meßgerät entladen sind. Dies betrifft besonders Elektrolytkondensatoren, bei denen man darüber hinaus auf die Polarität achten sollte. Obwohl sicher kaum ein Elko von falsch gepolten 3,3 V Schaden nimmt (höher wird die Meßspannung nicht), wird doch der Kapazitätswert verfälscht. Elkos werden im empfindlicheren Meßbereich wegen des Leckstroms generell eine höhere Kapazität vortäuschen als im unempfindlicheren.
Fehlerrechnung zur Schaltung in Bild 3
Stückliste zur Schaltung in Bild 3
Stückliste zur Schaltung in Bild 4
HTML-Code geprüft und für korrekt befunden:
- Grundlagen - Genauer! - Aufbau - Abgleich

